reveal.js

Before you start:

Allow video autoplay of the browser

Assessing chemical preference of young zebrafish

Benjamin Gallois

I. FastTrack: a general purpose tracking software

Image-based tracking

Locating objects over time from a video recording.

Challenges

Object detection
Complex object interactions
Trade-off accuracy / specialization
Trade-off accuracy / speed

Tracking in the lab

Simplifications:

Controlled lighting
Uniform background
Good image quality
Often quasi 2D

Requirements:

Low fault tolerance
Minimal human interventions
Versatile

Existing software

Properties-based

Use dynamic properties to keep the identities (Rodriguez, Alvaro, et al. 2018)

Fast
Error propagation

Individuals-based

Extract a fingerprint for each individual (Romero-Ferrero, Francisco, et al. 2019)

Computationally intensive
Close to perfect accuracy

Two-Dimensional tracking Dataset

41 movies under CC BY-NC-SA 4.0 license
7 animal species (from cells to mice)
Active particles
Microfluidic droplets
Macrocopic objects
http://chat.ljp.upmc.fr/datasets/TD2/

FastTrack: a general tracking software

Fast and automatic tracking algorithm
Ergonomic correction tool

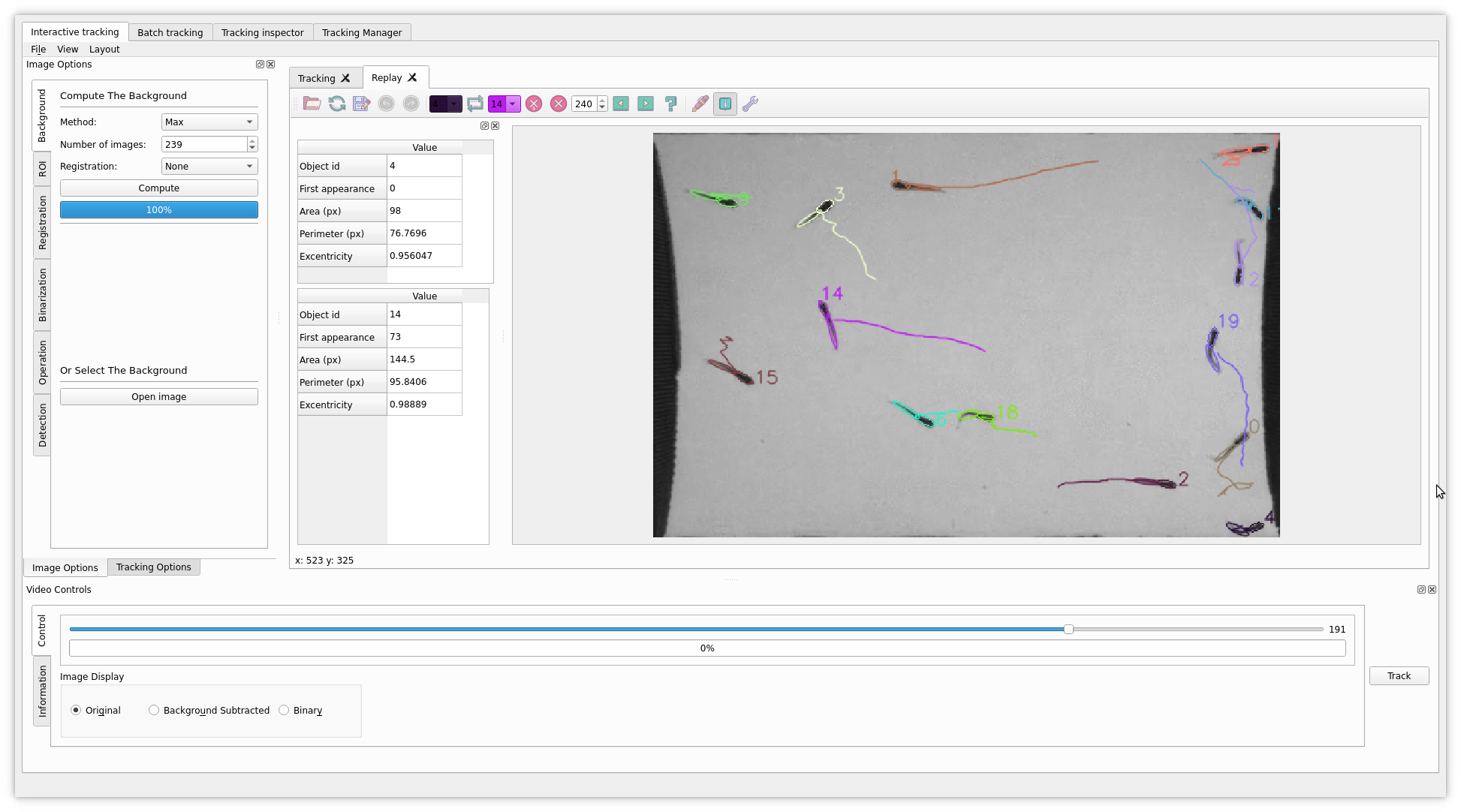
Detection

Matching

Keep the identity of the objects from one image...

Matching

To the next.

Matching

$$c_{11}=\frac{d_{11}}{s_d} + \frac{a_{11}}{s_a}$$

Matching

$$c_{12}=\frac{d_{12}}{s_d} + \frac{a_{12}}{s_a}$$

Matching

$$c_{13}=\frac{d_{13}}{s_d} + \frac{a_{13}}{s_a}$$

Matching

$$C = \begin{bmatrix} c_{11} & c_{12} & c_{13}\\ & & \\ & & \end{bmatrix}$$

Matching

Soft cost

$$c_{ij} = \frac{\delta d_{ij}}{s_d} + \frac{\delta a _{ij}}{s_{a}} + \frac{...}{...}$$

Hard cost

Distance: if $d_{ij}>h_d$, then $c_{ij} = \infty$
Memory: if object $i$ lost more than $h_t$ time, then remove the $i^{th}$ line

Global optimization

Best assignment possible using Hungarian algorithm (J. Munkres, 1957)

Post processing

Keyboard and mouse shortcuts
Swap, delete ids
Annotation frame by frame (Sturman, Oliver, et al., 2020)

Performance

Dataset classification

Metric to classify tracking difficulty
Does not necessitate groundtruth trajectories
Robust to tracking errors

Incursion

Incursion: object exits its Voronoï cell defined at a time $t$, after a travel time $\tau$.

Reduced displacement

Reduced displacement $\rho=r\sqrt{d}$

Typical distance to neighbors $\rho=1$
Typical distance to Voronoï cell edges $\rho=\frac{1}{2}$

Geometric probability of incursion

Geometric probability of incursion: proportion of angles for which incursions occur for a given displacement $\rho$.

Per Voronoï cell

$$p(\rho)=\frac{\color{red}{\Sigma_{out}(\rho)}}{\color{red}{\Sigma_{out}(\rho)} \color{black}{+}\color{blue}{\Sigma_{in}(\rho)}} $$ $$p(\rho)=\frac{\color{red}{\Sigma_{out}(\rho)}}{2\pi}$$

Geometric probability of incursion

To account for many shapes and sizes:

$$p_{inc}(\rho)=\left< p(\rho) \right>_{cells}$$

Probability of incursion

If the dynamics is uncorrelated with the geometric properties of the Voronoï cells: $$\color{green}{P_{inc}} = \int_{0}^{\infty} \color{blue}{R(\rho)} \color{red}{p_{inc}(\rho)} \,d \rho $$

$P_{inc}$ probability of incursion
$R(\rho)$ distribution of displacements at the timescale $\tau$
$p_{inc}(\rho)$ geometric probability of incursion

Probability of incursion

At $\tau=1$, $P_{inc}$ highly sensitive to tracking errors that shift $R(\rho)$ to the right.

Timescale analysis

$$P_{inc} = \frac{L}{1 + exp(-k .log(\frac{\tau}{\tau_0}))}$$

Timescale analysis

$$\delta = \frac{N_{err}}{N_{obj}}$$

Insensitive up to 1 error every 1000 detections.

Timescale analysis

ZFJ_001 very difficult movie: $$\delta \approx 0.003$$ without post-processing.

Optimal framerate

Oversampled: lot of storage space, higher processing time
Undersampled: lot of incursions, higher post-processing time

Define $\tau_1$ the timescale at which the incursion probability is equal to a single incursion in the whole movie.

$\tau_1<1$: undersampled
$\tau_1>1$: oversampled

Conclusion

Easy to install
Available on Linux, MacOS and Windows
Versatile
Open-source & API documented

New measure of trackability with $P_{inc}$
$\tau_1$ a criterion to find the optimal experimental framerate

II. Assessing chemical preference of young zebrafish

Chemical perception

(Hara, Toshiaki J., 2012) (Yarmolinsky, David A., Charles S. Zuker, and Nicholas JP Ryba, 2009)

Most ancien sensory system dating back 500 millions years ago
Wide range of taxa: unicellular to mamalian
Highly conservated features
Mediate feeding and reproduction

Olfaction

(Laberge, Frédéric, and Toshiaki J. Hara., 2001)

Olfactory epithelium (snout) projecting into the olfactory bulb (brain)
Mediate feeding, reproduction, fright reaction

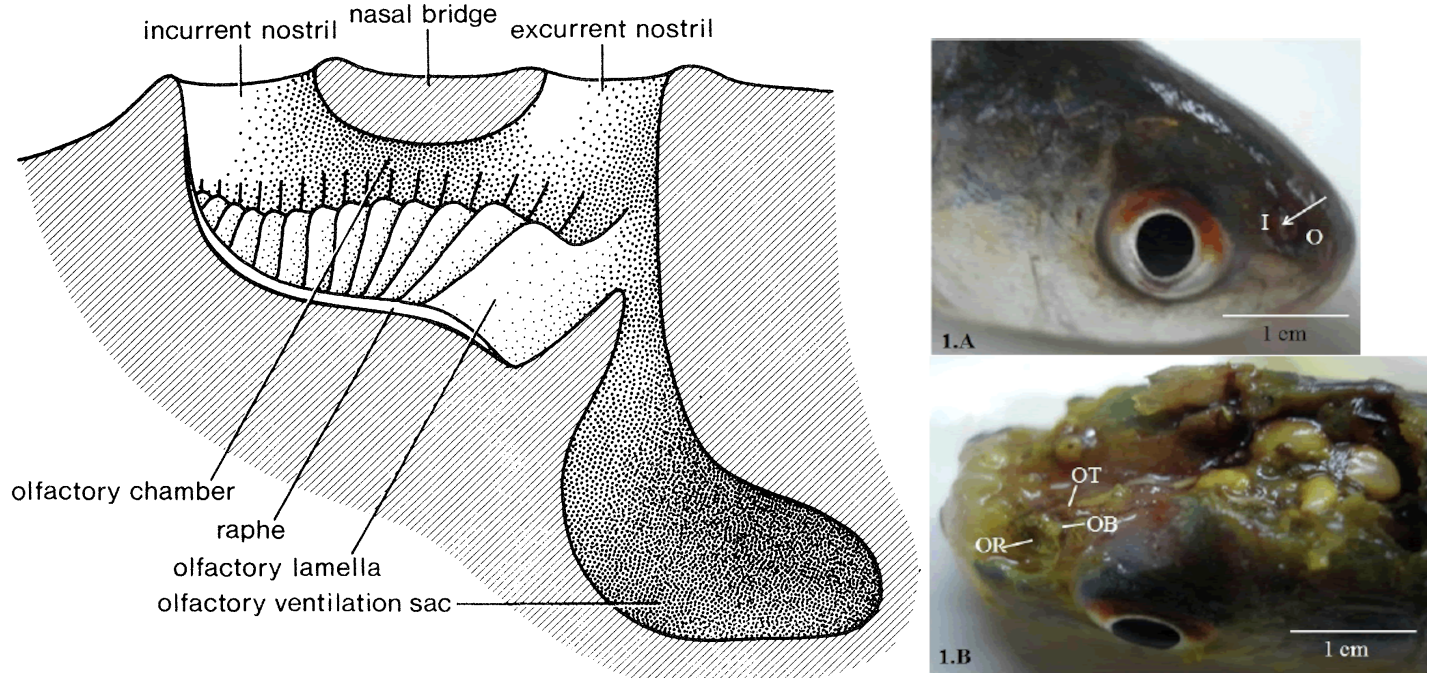
Gustation

Taste buds located on the head, lips, oropharyngeal cavity and barbels
Mediate feeding, reproduction

Common chemical sense

Solitary chemosensory cells in the epidermis

The zebrafish

Small and robust vertebrate
Well studied chemical senses: first odor responses $\approx$ 3 dpf (Li, Jun, et al., 2005)
Various behaviors: phototaxis, OMR, predation
Whole brain imaging using lightsheet microscopy and transgenic larval fish(Panier, Thomas, et al., 2013)

Zebrafish phototaxis

Light-seeking navigation
Spatial & temporal phototaxis
Map behavior onto a neuronal model

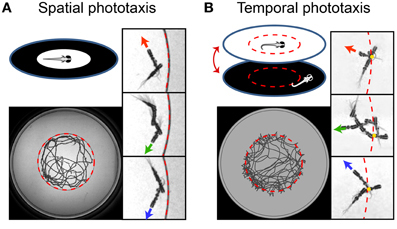(Chen, Xiuye, and Florian Engert, 2014)

(Karpenko, Sophia, et al., 2020)

Chemical perception

Biological noise
Chemical noise: intermittency, concentration variations
Moths, mosquitoes: plume structure, concentration independent (Mafra‐Neto, A., and R. T. Cardé., 1995)(Dekker, Teun, Willem Takken, and Ring T. Cardé., 2001)